Minimax ve XoX Oyunu (Yabancılar Tic Tac Toe diyor)

Oyun Ağaçları: Oyun ağacı bir oyundaki (bizim şu anki hedefimiz iki kişilik mantık oyunlarıdır) hamleleri gösteren yapıdır. Başlangıç pozisyonu ağacın köküdür. Herhangi bir düğümün herhangi bir çocuğuna tek bir oyun hamlesi ile erişmek mümkündür. Aşağıdaki resimde Tic Tac Toe oyunu olarak bilinen (Benim XOX olarak bildiğim) oyunun oyun ağacı görülmektedir. Şekilden de anlaşıldığı gibi bir kökümüz ve bu düğümlerden tek hamleyle erişebildiğimiz farklı dallarımız (çocuklarımız) vardır. Minimax algoritmasında bizim temel yardımcımız bu oyun ağacı yapısıdır. O yüzden oyun ağacı kavramını iyice öğrenmemiz gereklidir.

Minimax: Altüst adı da verilen bu yöntem (minimaksta denilebiliyor) zeka (mantık) oyunlarında sıklıkla kullanılan bir yapay zeka tekniğidir. Bu yöntemin kullanılabilmesi için aşağıdaki şartların sağlanması gerekmektedir:

• İki kişilik olmalıdır
• Sırayla oynanmalıdır. (Bir 1. oyuncu bir 2. oyuncu şeklinde)
• Oyun durumu ilgili bilgiyle birlikte tahta olarak temsil edilebilmelidir.
• İki oyuncuda sonraki olası hamlelerin hepsi hakkında bilgiye sahip olmalıdır. Buna mükemmel bilgi (“perfect knowledge”) denilmektedir. Örneğin Poker bu duruma uymaz. Rakibimizin elindeki kartları bilemeyiz.
• Oyun hamleleri rasgele olmamalıdır. (Zar oyunları dışarıda kalmaktadır)
• Oyunlar sonlu olmalıdır. Bir şekilde bitiş durumu olmalıdır.

Minimax yöntemi yukarıdaki şartları sağlayan oyunlar için bir arama yöntemidir. Bu arama daha önce bahsettiğimiz oyun ağacı üzerinde en uygun hamlenin bulunmasına yönelik bir aramadır.

Tic Tac Toe oyunu: Bu oyunu bildiğinizi düşünüyorum. Ama eğer bilmiyorsanız şimdi size anlatacağım.

Tic tac toe oyununda (ben bundan sonra buna XOX demek istiyorum) 3X3 bir tahtaya sahipsiniz. Ve oyunculardan ilki X, ikincisi O hamlesini oynayabilmektedir. Kağıt kalemle bile oynayabildiğimiz bu oyunda sınıfta derste sıkıldığınız zaman oynayabilirsiniz. Boş kağıt üzerinde çok büyük olmayan bir 3X3’lük matris (bunu bildiğinizi varsayıyorum) çizersiniz, bu matriste ilk başlayan oyuncu boş bir kareye X yazarak, diğer oyuncuda boş karelerden birine O yazarak hamlelerini sırasıyla oynarlar. Satırlarda, sütunlarda ve köşegenlerde aynı karakterleri (XXX veya OOO şeklinde) sağlayan ilk oyuncu oyunu kazanır. Eğer boş alan kalmazsa oyun berabere tamamlanmış olur. Bu oyunla ilgili önemli bir anekdot War Games filminde filmin sonunda (ben sadece sonunu izledim :D ) bilgisayarın nükleer saldırısını (ya da öyle bir şey) önlemek için çocuk bilgisayara karşı bu oyunu kazanmak zorunda, elbette ilk hamle bilgisayarda olunca kazanmak zor oluyor, bu nedenle oynamamayı tercih ediyor ve hatta "A strange game. The only winning move is not to play. How about a nice game of chess?" ("İlginç bir oyun. Kazanan tek hamle oynamamak. Güzel bir satranç oyununa ne dersin?") şeklinde bir cümlede filmde geçiyor. Gerçi filmin yapıldığı yılda tahminimce bilgisayarların satrançta dünya ustasını yenebileceğine bile inanılmıyordu.

Neyse konuyu fazla dağıtmayalım.(Oyunu anladığınızı umuyorum anlamadıysanız anlamış gibi davranın ya da şuradan bir deneyin.)

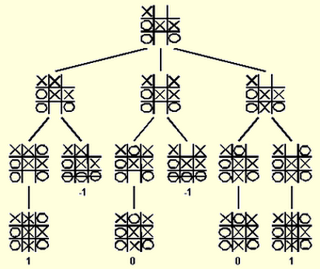
Minimax yöntemindeki düşünce oyun ağacında rakibin en iyi hamleleri oynayacağı (MAX) bizim ise en kötü hamleleri (MIN) oynayacağımızdır. Bu şartlarda ağaçta dallar (çocuklar) incelenerek en iyi hamle bulunmaya çalışılır. Aşağıdaki şekil incelenirse ne anlatmaya çalıştığım daha iyi anlaşılacaktır:

Şekilden de görülebildiği gibi 1. oyuncunun hamlesi sonucu kökümüz oluşmuş durumda. Bu köke bağlı çocuk düğümler yapraklar (bitiş noktası, çocuğu olmayan düğümler) elde edilene kadar oluşturulmakta ve bu düğümlerin değerleri hesaplanmaktadır. Daha sonra 1. oyuncunun hamlelerindeki değeri en küçük olanlar, ikinci oyuncunun hamlelerinde değerleri en büyük olanlar (bu değer hamlenin kalitesini belirtmektedir) seçilerek en uygun yol belirlenmektedir. Ve ikinci oyuncu için hamleyi belirlemiş oluyoruz. Bu hamlenin kazanç hamlesi olduğunu düşünüyoruz.

Yukarıdaki şekilde en altta bitiş yapraklarına kazanca göre değer verilmiştir. Altında -1, 1 ve 0 şeklinde oyun sonucu yazılan yapraklar bizim bitiş noktalarımızı temsil etmektedir. Tahta başlangıç pozisyonunda (şekildeki kök düğüm) yapılabilecek en iyi hamle olarak sıradaki oyuncunun kazanabileceği bir hamle seçilmelidir. Eğer sıradaki oyuncunun (-1 O, 1 X, 0 beraberlik) X olduğunu düşünürsek bu durumda yolu belirlemek için minimax yöntemini yukarıdaki ağaçta aşağıdaki şekilde kullanırsak aşağıdaki hesaplanmış ağacı elde ederiz:

Bu oluşan hesaplama sonucunda bizim için en iyi yolun en sağdaki yol olduğu açıkça ortaya çıkmaktadır. Bu elde ettiğimiz hamleye en iyi hamle adı verilmektedir. Ve sıradaki oyuncu için (bu durumda X) en iyi hamle sağdaki dalı takip etmesidir. Bu dalı takip ederek X oyuncusu en kötü ihtimalle bir beraberlik alacaktır.

Gerçekleştirim: Minimax algoritmasını aşağıdaki şekilde gerçekleştirdim. Burada size sadece minimax gerçekleştirimini yazdığım sınıfı göstereceğim. Tüm kodlarımı incelemek isterseni aşağıdaki kaynak kodları indirip eclipse projesi olarak açabilirsiniz.

package net.tekrei.xox;

public class YZ {

 public static Hamle getHamle(byte[] tahta, Hamle onceki) {
  // Hamleyi dugum olarak yaratalim
  Dugum root = new Dugum(tahta, onceki);
  // Karsilastiracagimiz deger
  byte max = Byte.MIN_VALUE;
  // Bulunmasini umdugumuz en iyi hamlenin dugumu
  Dugum enIyiDugum = null;
  // Tahta henuz dolmamissa
  if (!Tahta.dolu(tahta)) {
   // Kokteki her cocuk icin
   Dugum[] children = root.getCocuklar();
   // Minimax hesaplamasi yapalim
   for (int i = 0; i <>length; i++) {
    // Ilk olarak max yapmaliyiz
    // minimax bir ozyinelemeli bir metod ve bir max bir min ilk basta max olacak
    // sekilde hesaplama yapmalidir
    byte val = minimax(children[i], false);
    // Eger en son dugumun degeri elimizdekinden buyuk ise degistir
    if (val > max) {
     max = val;
     // ve en iyi dugum olarak al
     enIyiDugum = children[i];
    }
   }
   // en iyi dugumun hamlesini dondur
   return enIyiDugum.getHamle();
  } else {
   // Tahta dolmus haberimiz yok
   return null;
  }
 }

 private static byte minimax(Dugum d, boolean min) {
  // Yaprak ise degerini dondur
  if (d.yaprak()) {
   return d.getDeger();
  }

  if (min) {
   // Minimum hesaplamasi
   return min(d);
  } else {
   // Maksimum hesaplamasi
   return max(d);
  }
 }

 private static byte max(Dugum d) {
  byte sonuc = Byte.MIN_VALUE;
  Dugum[] children = d.getCocuklar();
  for (int i = 0; i <>length; i++) {
   byte val = minimax(children[i], true);
   if (val > sonuc) {
    sonuc = val;
   }
  }
  return sonuc;
 }

 private static byte min(Dugum d) {
  byte sonuc = Byte.MAX_VALUE;
  Dugum[] children = d.getCocuklar();
  for (int i = 0; i <>length; i++) {
   byte val = minimax(children[i], false);
   if (val <>
    sonuc = val;
   }
  }
  return sonuc;
 }
}

Kaynak Kodlar Çalıştırılabilir Jar

Kaynaklar (İngilizce):
http://ai-depot.com/LogicGames/MiniMax.html
http://delphiforfun.org/Programs/NIM_Minimax.htm
http://bluebones.net/tictactoe/
Artificial Intelligence A Modern Approach
http://en.wikipedia.org/wiki/WarGames
http://www.gamasutra.com/features/20000626/brockington_pfv.htm (resimleri buradan aldım)
Minimaksı anlamak için bir applet

Kaynaklar (Daha doğrusu konu ile ilgili bağlantılar) (Türkçe):
http://sozluk.sourtimes.org/show.asp?t=minimaks
http://www.fazlamesai.net/index.php?a=article&sid=1477
http://www.bilgidata.com/localhost/bilgidata/yazi.jsp@dosya=a_altust_algoritmasi.xml.html
http://www.geocities.com/akadirbali/yapayzeka/bolum3.htm#335


Not : Herhangi bir konuda takılırsanız veya kodumla ilgili hata, daha iyi çözümler bulabilirseniz bana yorum yazarak bilgi veriniz.

Not 2: Beklenmeyen kötü bir hamle oynayabiliyor. Bunun üzerinde çalışıyorum. Bu konulardaki yorumlarınıza da açığım. :)

Not 3: Sonraki aşama bu oyunu python ve glade kullanarak Ubuntu GNU/Linux GTK üzerinde çalıştırmak. Orada da arayüzü halletmiştim.